Como mecanismo de transmissão, a engrenagem planetária é amplamente utilizada em diversas aplicações de engenharia, como redutores de engrenagens, guindastes, etc. No caso de redutores planetários, ela pode substituir o mecanismo de transmissão de engrenagens de eixo fixo em muitas situações. Como o processo de transmissão por engrenagens envolve contato linear, o engrenamento prolongado pode causar falhas nas engrenagens, sendo necessário simular sua resistência. Li Hongli et al. utilizaram o método de engrenamento automático para gerar a malha da engrenagem planetária e obtiveram resultados lineares em relação ao torque e à tensão máxima. Wang Yanjun et al. também geraram a malha da engrenagem planetária por meio do método de geração automática e realizaram simulações estáticas e modais da engrenagem planetária. Neste artigo, elementos tetraédricos e hexaédricos são utilizados principalmente para dividir a malha, e os resultados finais são analisados ​​para verificar se as condições de resistência são atendidas.

1. Estabelecimento do modelo e análise dos resultados

Modelagem tridimensional de uma engrenagem planetária

Engrenagem planetáriaÉ composto principalmente por engrenagem anular, engrenagem solar e engrenagem planetária. Os principais parâmetros selecionados neste trabalho são: o número de dentes da engrenagem anular interna é 66, o número de dentes da engrenagem solar é 36, o número de dentes da engrenagem planetária é 15, o diâmetro externo da engrenagem anular interna é 150 mm, o módulo é 2 mm, o ângulo de pressão é 20°, a largura do dente é 20 mm, o coeficiente de altura do adendo é 1, o coeficiente de folga é 0,25 e há três engrenagens planetárias.

Análise de simulação estática de engrenagem planetária

Defina as propriedades do material: importe o sistema de engrenagens planetárias tridimensional desenhado no software UG para o ANSYS e defina os parâmetros do material, conforme mostrado na Tabela 1 abaixo:

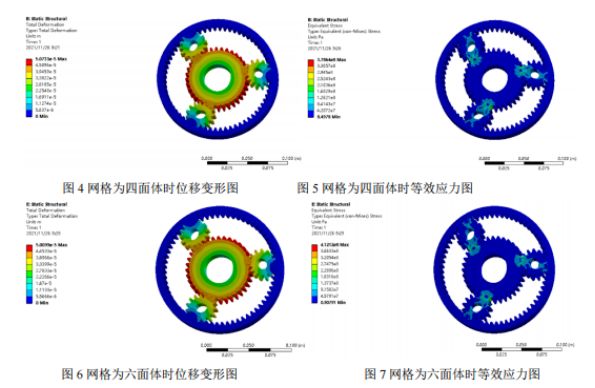
Malha: A malha de elementos finitos é dividida em tetraedros e hexaedros, e o tamanho básico do elemento é de 5 mm. Como oengrenagem planetáriaA engrenagem solar e o anel da engrenagem interna estão em contato e engrenados, a malha das partes de contato e engrenadas é densa e tem tamanho de 2 mm. Primeiro, são utilizadas malhas tetraédricas, como mostrado na Figura 1. São gerados 105.906 elementos e 177.893 nós no total. Em seguida, adota-se uma malha hexaédrica, como mostrado na Figura 2, e são geradas 26.957 células e 140.560 nós no total.

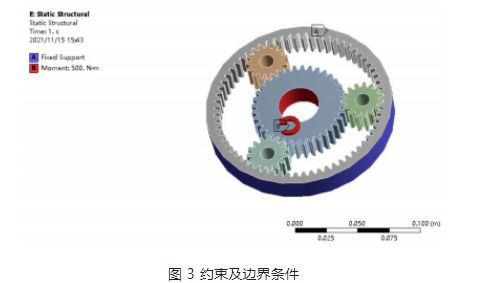
Aplicação de carga e condições de contorno: de acordo com as características de funcionamento da engrenagem planetária no redutor, a engrenagem solar é a engrenagem motora, a engrenagem planetária é a engrenagem movida e a saída final é feita através do porta-satélites. Fixe a coroa da engrenagem interna no ANSYS e aplique um torque de 500 N·m à engrenagem solar, conforme mostrado na Figura 3.

Pós-processamento e análise de resultados: O nefrograma de deslocamento e o nefrograma de tensão equivalente da análise estática obtidos a partir de duas divisões da malha são apresentados abaixo, e uma análise comparativa é realizada. A partir do nefrograma de deslocamento dos dois tipos de malha, verifica-se que o deslocamento máximo ocorre na posição onde a engrenagem solar não engata com a engrenagem planetária, e a tensão máxima ocorre na raiz do engrenamento da engrenagem. A tensão máxima da malha tetraédrica é de 378 MPa, e a tensão máxima da malha hexaédrica é de 412 MPa. Como o limite de escoamento do material é de 785 MPa e o fator de segurança é de 1,5, a tensão admissível é de 523 MPa. A tensão máxima em ambos os resultados é inferior à tensão admissível, e ambos atendem às condições de resistência.

2. Conclusão

Por meio da simulação de elementos finitos da engrenagem planetária, obtêm-se o nefrograma de deformação por deslocamento e o nefrograma de tensão equivalente do sistema de engrenagens, a partir dos quais são determinados os dados máximos e mínimos e sua distribuição no sistema.engrenagem planetáriaÉ possível encontrar um modelo. A localização da tensão equivalente máxima também é a localização onde os dentes da engrenagem têm maior probabilidade de falhar, portanto, deve-se prestar atenção especial a ela durante o projeto ou a fabricação. Através da análise de todo o sistema de engrenagem planetária, o erro causado pela análise de apenas um dente da engrenagem é superado.